コインを作って大きな数の計算をしてみよう

＜準備するもの＞

・折り紙　6枚
・はさみ
・ペン
・液体のり

＜十円玉を作ろう＞

まずは十円玉を作ってみましょう。十円玉にしたい色の折り紙を1枚と、中に入れるための折り紙1枚を準備します。中に入れる折り紙は見えなくなりますので何色でもいいでしょう。

①折り紙を十六等分します

折り紙をたて向きに二等分、それをさらに二等分して四等分します。次に横向きに二等分、それをさらに二等分して四等分します。開くと写真のような折り紙を十六等分する折り筋がついています。

②折り紙を切ります

十六等分のマス目を2個ずつで切り分けます。切り分けた1個は八等分の広さになっています。

③円を切り取ります

八等分した折り紙を2つに折り、折った側が少しつながるように円を描きます。コンパスを使っても良いですが、使わずにだいたいの円が描ければ良いでしょう。

④「10」と書きます

円の真ん中に「10」と書きます。両面に書いて下さい。

⑤中に入れる折り紙を切ります

折り紙を同じ方向に3回折って八等分の折り筋をつけ、折り筋の通りに切ります。

⑥正方形にたたみます

短冊状の折り紙を同じ方向に3回折って正方形にたたみます。中に入れると見えなくなるので、どちらの面を表にしても良いです。

⑦中に折り紙を入れます

円に切った折り紙に挟み込むように正方形にたたんだ折り紙を入れます。円のふちにのりをつけて円を閉じると十円玉ができあがります。同じように、一円玉や百円玉も作りましょう。中に折り紙を入れることで厚みがでるので遊びやすくなります。

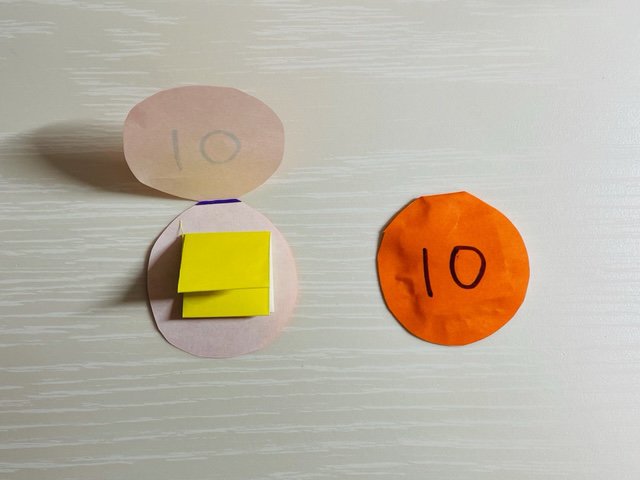
＜何十、何百のたし算とひき算に挑戦しよう＞

「50＋30」を考えてみます。式を見るだけだと2けたのたし算ですが、十円玉の枚数で考えると1けたの計算になります。十円玉が5枚と3枚なので「5＋3＝8」で8枚となり、お金の価値を考えると結果は80円になります。同じように「70－50」などのひき算にも挑戦してみましょう。また百円玉を使って「300＋400」や「900－300」などの計算も考えてみてください。

＜何十、何百のかけ算に挑戦しよう＞

「30×3」の計算について十円玉を使って考えてみましょう。30円は十円玉が3枚と考えるとそれが3組あります。枚数で考えると「3×3＝9」で9枚というようにかけ算九九で考えることができます。お金の価値を考えると90円になりました。

この計算の方法の説明としては、「30のゼロをとって3×3を計算し、最後にゼロをつける」というものをよく聞きます。確かに操作としてはその通りなのですが、意味がともなわない操作の暗記は忘れてしまうと全く考えることができなくなります。「ゼロをとるということはコインの枚数で考えている」と知っておけば、忘れてしまうこともないでしょう。

同じように「30×5」を考えてみます。十円玉の枚数で考えると3枚が5組、「3×5＝15」で15枚の十円玉があることになります。お金の価値を考えると150円になりました。

ここまでできた人は「200×4」や「800×4」などの計算も考えてみてください。

＜2けた×1けたのかけ算に挑戦しよう＞

「12×3」の計算に挑戦してみましょう。12を十円玉が1個、一円玉が2個と考えます。これが3組なので、まず1円玉の枚数を調べます。2円が3組ですから枚数で考えると「2×3＝6」で6枚になります。十円玉は1個が3組なので枚数は「1×3＝3」で3枚となり、30円ということがわかります。合わせると36円になります。

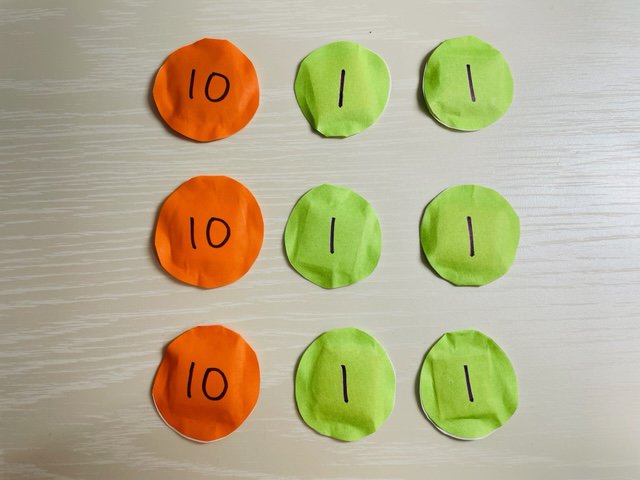
では「14×3」はどうでしょうか。14を十円玉が1個、一円玉が4個と考えると、これが3組ということになります。一円玉の枚数は、4円が3組なので枚数は「4×3＝12」で12枚となり、12円ということがわかります。十円玉は1個が3組なので枚数は「1×3＝3」で3枚、つまり30円となり、合わせると「12＋30＝42」で42円になりました。この考え方は、かけ算のひっ算で行われることと同じなのでぜひ確かめてみてください。

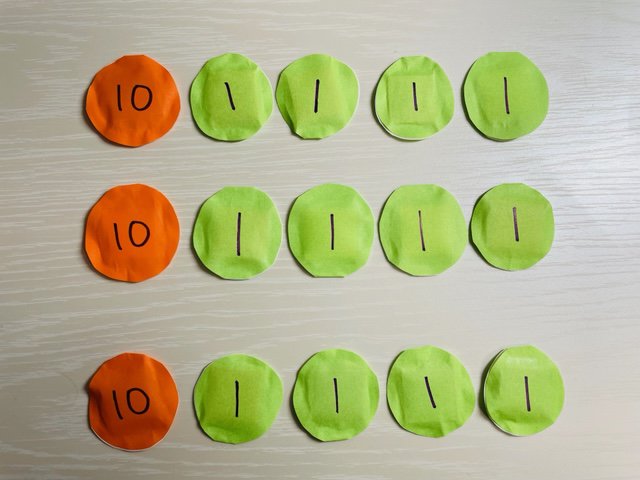
また、このような「2けた×1けた」や「3けた×1けた」などの計算はひっ算を使わずに計算できるとよいでしょう。なぜなら、2けたや3けたでわる、わり算のひっ算の時にも必要になる計算だからです。

自分で作ったコインを使って、楽しみながら計算の意味を知ることができると良いですね。